README.md

参考文献

前言

这个文档的初衷是记录书中引用文献的链接， 但是后来这个被Downloader做了， 可以自动下载所有文献到refs文件夹。

在review02的时候，发现书中的文献有些可圈点，或精读，或略读，或以后再读，都需要个文档来记录，就在这个文档的基础上做这个事情吧。

本文中的文献不限于《统计学习方法》中引用的范围， 扩充的一些会有一定的说明。

CH01 统计学习方法概论

1. 0
2. 0
3. Bishop, 2006 PRML 这本书火的不得了
4. Brian, 1996 PRNN 这本书早发十年, 不火. 居然早发了十年, 只有英文版本, 没有中文翻译.

CH04 朴素贝叶斯法

1. Mitchell TM, 2017 这是机器学习第二版的手稿，这部分讲的内容很经典，推荐阅读。在Refs里面做了翻译笔记
2. ESL 书中说的是关于朴素贝叶斯法的介绍，这本书中有描述，但是，暂时没找到。后面再详细看。

CH06 逻辑斯谛回归与最大熵模型

1. Berger, 1996

   书中6.1的例子来自这里， 文章讲述的是Maxent在NLP里面的应用， 例子给出的是法语到英语的翻译。

   在文献中, 还包含了Feature Selection部分, 在书中并没有对应的体现, 可以细看一下.

CH08 提升方法

9. Schapire， 2004

   这个文章里面说明了AdaBoost和LR的关系。

   LR中的feature对应了AdaBoost中的weak或者base hypotheses

   文献中还有包含了多分类问题， 一提到多分类， 有OvO， OvR，但是AdaBoost的多分类形式有好多版本， 跨度两三年。所以， 讲讲道理容易，和具体的实现还是有差异的。

CH09 EM算法及其推广

1. Dempster, 1977 maximum-likelihood from incomplete data via the em algorithm 不完全数据

CH10 隐马尔可夫模型

1. Rabiner, 1986 本书HMM部分的符号体系和这个文章是一样的, 参考文件的第一二文章和第九章的最大熵的文章差不多, 经典. 文章较长, 讨论的较全面.
2. Bilmes, 1997 书中review了最大似然，这是本章的大参考文献。符号体系不是太一样，这里面我觉得比较好的是状态用了$q$这样不会出现$i_i$的情况。讲解了GMM和HMM中应用EM算法进行参数估计的过程。另外学到了一个关于省略数学推导的金句we try to emphasize intuition rather than mathematical rigor.

CH11 条件随机场

其他

1. Zhangtong, 2001, Statistical Behavior and Consistency of Classification Methods based on Convex Risk Minimization

   文章中有AdaBoost和LR的损失函数对比，从凸风险最小化的角度来分析这些算法。和CH06，CH07,CH08都有关系。文章中损失函数用$\phi$表示。

   从距离的角度看， 逻辑回归的度量函数是KL散度，也就是相对熵。

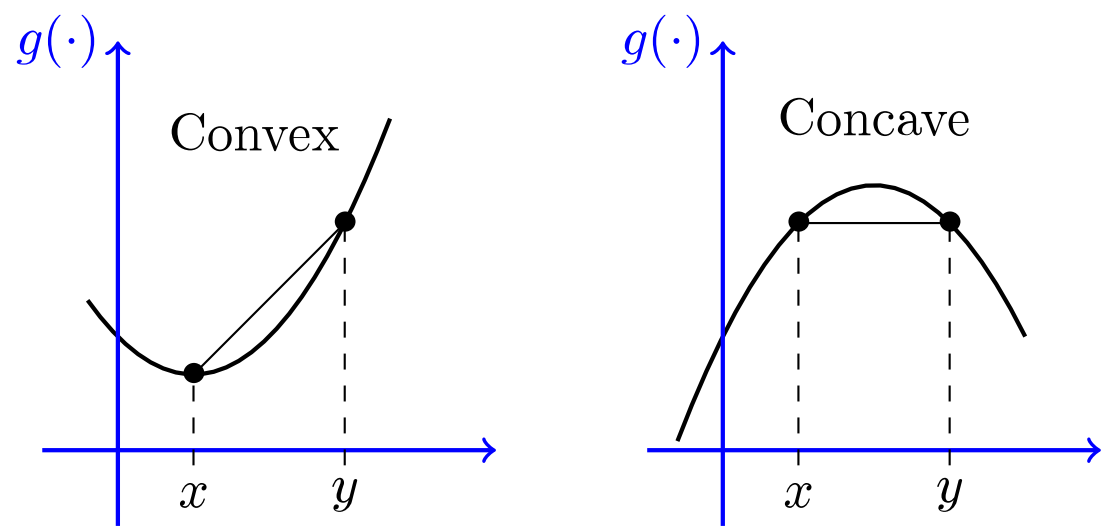
   在定义Bregman Divergence的时候，文献中提到了convex和concave，下面引用两个图片。

   

   图片来自， https://math.stackexchange.com/questions/2364116/how-to-remember-which-function-is-concave-and-which-one-is-convex

   

   图片来自https://www.grammarly.com/blog/concave-vs-convex/

   Bregman Divergence 非负。