Interviews
Your personal guide to Software Development technical interviews.
Maintainer - Kevin Naughton Jr.
- A Linked List is a linear collection of data elements, called nodes, each pointing to the next node by means of a pointer. It is a data structure consisting of a group of nodes which together represent a sequence.
- Singly-linked list: linked list in which nodes have pointers to the next node
- Doubly-linked list: linked list in which nodes have pointers to both the previous node and the next node
- Time Complexity:
- Access:
O(n) - Search:
O(n) - Insert:
O(1) - Remove:
O(1)
- Access:
- A Stack is a collection of elements, with two principle operations: push, which adds to the collection, and pop, which removes the most recently added element
- Last in, first out data structure (LIFO)
- Time Complexity:
- Access:
O(n) - Search:
O(n) - Insert:
O(1) - Remove:
O(1)
- A Queue is a collection of elements, supporting two principle operations: enqueue, which inserts an element into the queue, and dequeue, which removes an element from the queue
- First in, first out data structure (FIFO)
- Time Complexity:
- Access:
O(n) - Search:
O(n) - Insert:
O(1) - Remove:
O(1)
- A Tree is an undirected, connected, acyclic graph
- A Binary Tree is a tree data structure in which each node has at most two children, which are referred to as the left child and right child
- Full Tree: a tree in which every node has either 0 or 2 children
- Perfect Binary Tree: a binary tree in which all interior nodes have two children and all leave have the same depth
- Complete Tree: a binary tree in which every level except possibly the last is full and all nodes in the last level are as far left as possible
- A binary search tree, sometimes called BST, is a type of binary tree which maintains the property that the value in each node must be greater than or equal to any value stored in the left sub-tree, and less than or equal to any value stored in the right sub-tree
- Time Complexity:
- Access:
O(log(n)) - Search:
O(log(n)) - Insert:
O(log(n)) - Remove:
O(log(n))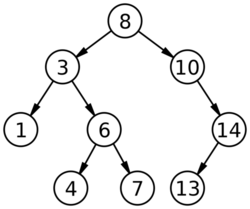
- A Heap is a specialized tree based structure data structure that satisfies the heap property: if A is a parent node of B, then the key (the value) of node A is ordered with respect to the key of node B with the same ordering applying across the entire heap. A heap can be classified further as either a "max heap" or a "min heap". In a max heap, the keys of parent nodes are always greater than or equal to those of the children and the highest key is in the root node. In a min heap, the keys of parent nodes are less than or equal to those of the children and the lowest key is in the root node
- Hashing is used to map data of an arbitrary size to data of a fixed size. The values return by a hash function are called hash values, hash codes, or simply hashes. If two keys map to the same value, a collision occurs
- Hash Map: a hash map is a structure that can map keys to values. A hash map uses a hash function to compute an index into an array of buckets or slots, from which the desired value can be found.
- Collision Resolution
- Separate Chaining: in separate chaining, each bucket is independent, and contains a list of entries for each index. The time for hash map operations is the time to find the bucket (constant time), plus the time to iterate through the list
- Open Addressing: in open addressing, when a new entry is inserted, the buckets are examined, starting with the hashed-to-slot and proceeding in some sequence, until an unoccupied slot is found. The name open addressing refers to the fact that the location of an item is not always determined by its hash value
- A Graph is an ordered pair of G = (V, E) comprising a set V of vertices or nodes together with a set E of edges or arcs, which are 2-element subsets of V (i.e. an edge is associated with two vertices, and that association takes the form of the unordered pair comprising those two vertices)
- Undirected Graph: a graph in which the adjacency relation is symmetric. So if there exists an edge from node u to node v (u -> v), then it is also the case that there exists an edge from node v to node u (v -> u)
- Directed Graph: a graph in which the adjacency relation is not symmetric. So if there exists an edge from node u to node v (u -> v), this does not imply that there exists an edge from node v to node u (v -> u)
- Stable:
No - Time Complexity:
- Best Case:
O(nlog(n)) - Worst Case:
O(n^2) - Average Case:
O(nlog(n))
- Mergesort is also a divide and conquer algorithm. It continuously divides an array into two halves, recurses on both the left subarray and right subarray and then merges the two sorted halves
- Stable:
Yes - Time Complexity:
- Best Case:
O(nlog(n)) - Worst Case:
O(nlog(n)) - Average Case:
O(nlog(n))
- Bucket Sort is a sorting algorithm that works by distributing the elements of an array into a number of buckets. Each bucket is then sorted individually, either using a different sorting algorithm, or by recursively applying the bucket sorting algorithm
- Time Complexity:
- Best Case:
Ω(n + k) - Worst Case:
O(n<sup>2</sup>) - Average Case:
Θ(n + k)
- Radix Sort is a sorting algorithm that like bucket sort, distributes elements of an array into a number of buckets. However, radix sort differs from bucket sort by 're-bucketing' the array after the initial pass as opposed to sorting each bucket and merging
- Time Complexity:
- Best Case:
Ω(nk) - Worst Case:
O(nk) - Average Case:
Θ(nk)
- Depth First Search is a graph traversal algorithm which explores as far as possible along each branch before backtracking
- Time Complexity:
O(|V| + |E|)
- Breadth First Search is a graph traversal algorithm which explores the neighbor nodes first, before moving to the next level neighbors
- Time Complexity:
O(|V| + |E|)
- Topological Sort is the linear ordering of a directed graph's nodes such that for every edge from node u to node v, u comes before v in the ordering
- Time Complexity:
O(|V| + |E|)
- Dijkstra's Algorithm is an algorithm for finding the shortest path between nodes in a graph
- Time Complexity:
O(|V|^2)
- Bellman-Ford Algorithm is an algorithm that computes the shortest paths from a single source node to all other nodes in a weighted graph
- Although it is slower than Dijstra's, it is more versatile, as it is capable of handling graphs in which some of the edge weights are negative numbers
- Time Complexity:
- Best Case:
O(|E|) - Worst Case:
O(|V||E|)
- Floyd-Warshall Algorithm is an algorithm for finding the shortest paths in a weighted graph with positive or negative edge weights, but no negative cycles
- A single execution of the algorithm will find the lengths (summed weights) of the shortest paths between all pairs of nodes
- Time Complexity:
- Best Case:
O(|V|^3) - Worst Case:
O(|V|^3) - Average Case:
O(|V|^3)
.
├── Array
│ ├── bestTimeToBuyAndSellStock.java
│ ├── findTheCelebrity.java
│ ├── gameOfLife.java
│ ├── increasingTripletSubsequence.java
│ ├── insertInterval.java
│ ├── longestConsecutiveSequence.java
│ ├── maximumProductSubarray.java
│ ├── maximumSubarray.java
│ ├── mergeIntervals.java
│ ├── missingRanges.java
│ ├── productOfArrayExceptSelf.java
│ ├── rotateImage.java
│ ├── searchInRotatedSortedArray.java
│ ├── spiralMatrixII.java
│ ├── subsetsII.java
│ ├── subsets.java
│ ├── summaryRanges.java
│ ├── wiggleSort.java
│ └── wordSearch.java
├── Backtracking
│ ├── androidUnlockPatterns.java
│ ├── generalizedAbbreviation.java
│ └── letterCombinationsOfAPhoneNumber.java
├── BinarySearch
│ ├── closestBinarySearchTreeValue.java
│ ├── firstBadVersion.java
│ ├── guessNumberHigherOrLower.java
│ ├── pow(x,n).java
│ └── sqrt(x).java
├── BitManipulation
│ ├── binaryWatch.java
│ ├── countingBits.java
│ ├── hammingDistance.java
│ ├── maximumProductOfWordLengths.java
│ ├── numberOf1Bits.java
│ ├── sumOfTwoIntegers.java
│ └── utf-8Validation.java
├── BreadthFirstSearch
│ ├── binaryTreeLevelOrderTraversal.java
│ ├── cloneGraph.java
│ ├── pacificAtlanticWaterFlow.java
│ ├── removeInvalidParentheses.java
│ ├── shortestDistanceFromAllBuildings.java
│ ├── symmetricTree.java
│ └── wallsAndGates.java
├── DepthFirstSearch
│ ├── balancedBinaryTree.java
│ ├── battleshipsInABoard.java
│ ├── convertSortedArrayToBinarySearchTree.java
│ ├── maximumDepthOfABinaryTree.java
│ ├── numberOfIslands.java
│ ├── populatingNextRightPointersInEachNode.java
│ └── sameTree.java
├── Design
│ └── zigzagIterator.java
├── DivideAndConquer
│ ├── expressionAddOperators.java
│ └── kthLargestElementInAnArray.java
├── DynamicProgramming
│ ├── bombEnemy.java
│ ├── climbingStairs.java
│ ├── combinationSumIV.java
│ ├── countingBits.java
│ ├── editDistance.java
│ ├── houseRobber.java
│ ├── paintFence.java
│ ├── paintHouseII.java
│ ├── regularExpressionMatching.java
│ ├── sentenceScreenFitting.java
│ ├── uniqueBinarySearchTrees.java
│ └── wordBreak.java
├── HashTable
│ ├── binaryTreeVerticalOrderTraversal.java
│ ├── findTheDifference.java
│ ├── groupAnagrams.java
│ ├── groupShiftedStrings.java
│ ├── islandPerimeter.java
│ ├── loggerRateLimiter.java
│ ├── maximumSizeSubarraySumEqualsK.java
│ ├── minimumWindowSubstring.java
│ ├── sparseMatrixMultiplication.java
│ ├── strobogrammaticNumber.java
│ ├── twoSum.java
│ └── uniqueWordAbbreviation.java
├── LinkedList
│ ├── addTwoNumbers.java
│ ├── deleteNodeInALinkedList.java
│ ├── mergeKSortedLists.java
│ ├── palindromeLinkedList.java
│ ├── plusOneLinkedList.java
│ ├── README.md
│ └── reverseLinkedList.java
├── Queue
│ └── movingAverageFromDataStream.java
├── README.md
├── Sort
│ ├── meetingRoomsII.java
│ └── meetingRooms.java
├── Stack
│ ├── binarySearchTreeIterator.java
│ ├── decodeString.java
│ ├── flattenNestedListIterator.java
│ └── trappingRainWater.java
├── String
│ ├── addBinary.java
│ ├── countAndSay.java
│ ├── decodeWays.java
│ ├── editDistance.java
│ ├── integerToEnglishWords.java
│ ├── longestPalindrome.java
│ ├── longestSubstringWithAtMostKDistinctCharacters.java
│ ├── minimumWindowSubstring.java
│ ├── multiplyString.java
│ ├── oneEditDistance.java
│ ├── palindromePermutation.java
│ ├── README.md
│ ├── reverseVowelsOfAString.java
│ ├── romanToInteger.java
│ ├── validPalindrome.java
│ └── validParentheses.java
├── Tree
│ ├── binaryTreeMaximumPathSum.java
│ ├── binaryTreePaths.java
│ ├── inorderSuccessorInBST.java
│ ├── invertBinaryTree.java
│ ├── lowestCommonAncestorOfABinaryTree.java
│ ├── sumOfLeftLeaves.java
│ └── validateBinarySearchTree.java
├── Trie
│ ├── addAndSearchWordDataStructureDesign.java
│ ├── implementTrie.java
│ └── wordSquares.java
└── TwoPointers
├── 3Sum.java
├── 3SumSmaller.java
├── mergeSortedArray.java
├── minimumSizeSubarraySum.java
├── moveZeros.java
├── removeDuplicatesFromSortedArray.java
├── reverseString.java
└── sortColors.java
18 directories, 124 files