- This project involves self-avoiding random walks (commonly called “SAW”).
- A self-avoiding random walk is not allowed to intersect itself.
- To explain, consider a two-dimensional integer grid
- The random walk begins at the origin (0, 0).
- At each increment, the walk takes a step horizontally ±1 unit else vertically ±1 unit
- Diagonal steps are not allowed: each step is either horizontal else vertical.
- Suppose that after n steps, the path of the random walk is given by the set of points {(x0, y0),(x1, y1), . . . ,(xn, yn)}, where (x0, y0) = (0, 0).
- At the next step, the random walk goes to the point (xn+1, yn+1), which is one of the four possible points (xn + 1, yn), (xn − 1, yn), (xn, yn + 1) or (xn, yn − 1).
- However, it is forbidden for the point (xn+1, yn+1) to equal one of the points (x0, y0), . . . ,(xn, yn).
- Once a self-avoiding random walk passes through a point, it cannot pass through the same point again.
- Two or more points in the random walk are not allowed to coincide.
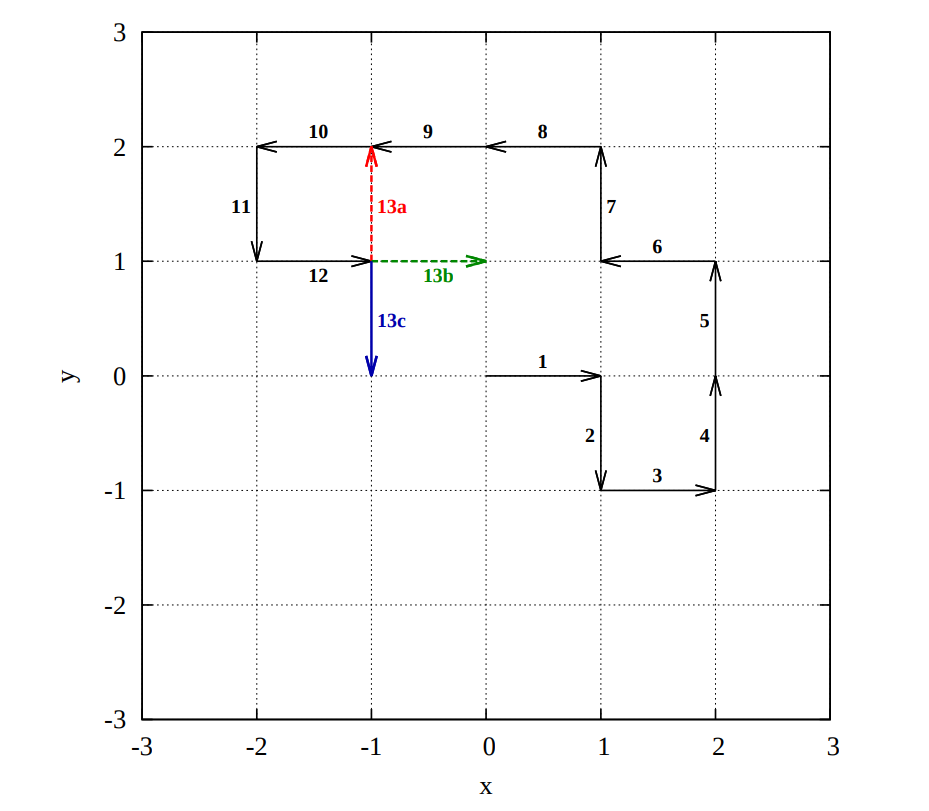
- An example of a self-avoiding random walk is displayed in Fig. 1.
- The walk starts at the origin (0, 0)
- Twelve steps are shown, labelled 1 through 12.
- After step 12, three possible steps labelled 13a, 13b and 13c are shown,
- The step labelled 13a is forbidden because the random walk would intersect itself
- The steps labelled 13b and 13c are allowed.
- Note that if the next step is 13b, then the random walk reaches a dead end, because all possible steps after that will self-intersect the path of the random walk.
- It is possible for a self-avoiding random walk to reach a dead end.
- There is one additional step after step 12, which is not displayed in Fig. 1.
- That is to reverse the direction of step 12 and go from (−1, 1) to (−2, 1).
- A “reverse step” is forbidden because it also counts as a self-intersection.
- In this project, we shall only consider self-avoiding random walks on integer grids.
- Every random walk always starts at the origin.
- Figure 1
- The mean (or average) of the end-to-end squared distance is given by the average:
- The mean (or average) of the end-to-end squared distance is given by the average:
- The mean (or average) of the end-to-end squared distance is given by the average:
