In this work, we proposed a modified version of Inverse Kinodynamic Learning for safe slippage and tight turning in autonomous drifting. We show that the model is effective for loose drifting trajectories. However, we also find that tight trajectories hinder the models performance and the vehicle undershoots the trajectory during test time. We demonstrate that data evaluation is an essential part of learning an inverse kinodynamic function, and that the architecture necessary to have success is simple and effective.

This work has the potential of becoming a stepping stone in finding the most effective and simple ways to autonomously drift in a life-or-death situation. Future work should focus on collecting more robust data, using more inertial readings and sensor readings (such as real-sense, other axes, or LiDAR). We have open-sourced this entire project as a stepping stone in these endeavors, and hope to explore our ideas further beyond this paper.

We denote $x$ as the linear velocity of the joystick, $z$ as the angular velocity of the joystick, and $z'$ as the angular velocity measured off of the IMU unit on the vehicle.

In the paper that inspired our work, the goal, generally, is to learn the function $f_{\theta}^{+}$ given the onboard inertial observations. More specifically, the paper formulates the function below:

$$f_{\theta}^{+}(\Delta{x}, x, y) \approx f^{-1}(\Delta{x}, x, y)$$

We can denote $x$ as the linear velocity of the joystick, $z$ as the angular velocity of the joystick, and $z'$ as the angular velocity measured by the IMU unit on the vehicle. We will denote our desired control input as $u_{z}$.

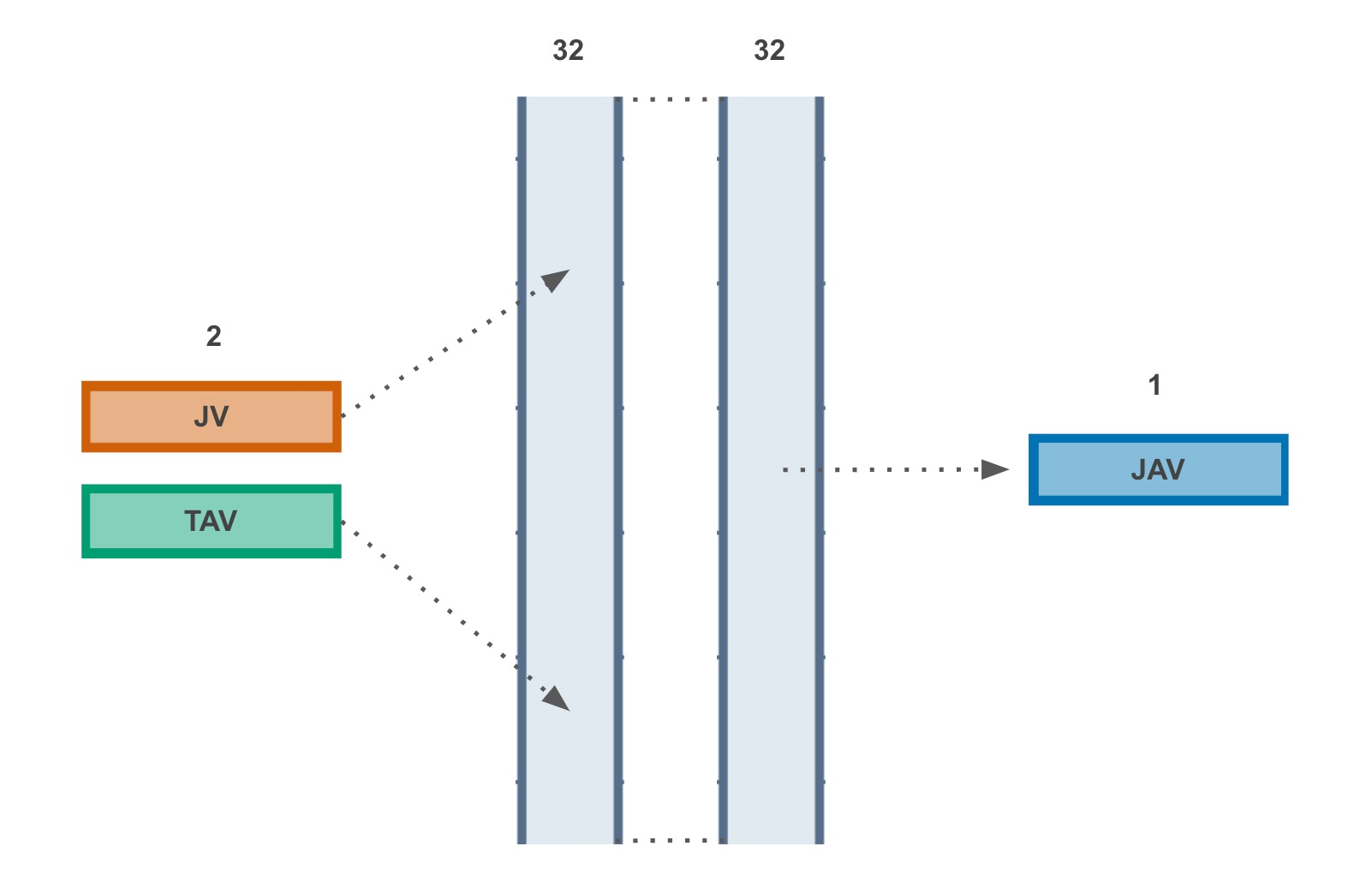
Our goal is to learn the function approximator $f_{\theta}^{+}$ based on the onboard inertial observations $z'$. $f_{\theta}^{+}$ then is used as our inverse kinodynamic model during test-time, in which it outputs our desired control input, $u_{z}$ to get us close to $z'$.

$$f_{\theta}^{+}: (x, z') \rightarrow {NN} \rightarrow z $$

Given enough real world observations: $f_{\theta}^{+} \approx f^{-1}$

$$(x, z) \rightarrow f^{-1} \rightarrow u_{z}$$

At training time, we feed two inputs into our neural network architecture, which is joystick velocity and ground truth angular velocity from the IMU on the vehicle. The output of this model is the predicted joystick angular velocity. The learned model is our learned function approximator, which is then used as test time as the inverse kinodynamic model to give us our desired control, a corrected angular velocity for the joystick $u_{z}$ that gets us closer to the observation in the real world, $z'$.